
Thus, χ 2 distribution depends on the degrees of distribution as its shape changes with the change in the ‘ν’, and as ‘ν’ becomes greater, χ 2 gets approximated by the normal distribution. The degrees of freedom for the three major uses are each calculated differently. (If you want to practice calculating chi-square probabilities then use df n1 d f n 1.

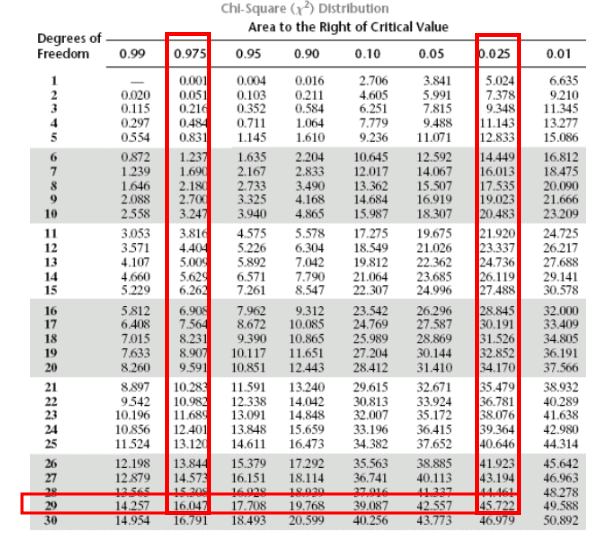
This property is called as the additive property of Chi-square. The notation for the chi-square distribution is 2 df d f 2, where df degrees of freedom which depends on how chi-square is being used. Suppose, χ 1 2 is a χ 2 variate with degrees of freedom ν 1 and χ 2 2 is another χ 2 variate with degrees of freedom ν 2, then their sum χ 1 2 + χ 2 2 will be equal to χ 2 variate with ν 1+ ν 2 degrees of freedom. The sum of independent χ 2 is itself a χ 2 variate. The chi-squared distribution is implemented in the Wolfram Language as ChiSquareDistribution n.Thus, the mean and standard deviation of the distribution of √2χ 2 is equal to √ 2ν-1 and one respectively. It has been determined that quantity √2χ 2 gives a better approximation to normality than the χ 2 itself if the values are about 30 or more. Therefore, Chi Square with one degree of freedom, written as 2(1), is simply the distribution of a single normal deviate squared. The χ2 distribution approaches the normal distribution as ν gets larger with mean ν and standard deviation as √2χ 2.While the variance is twice the degrees of freedom, Viz. The mean of the chi-square distribution is equal to the degrees of freedom, i.e.When ‘ν’ is small, the shape of the curve tends to be skewed to the right, and as the ‘ν’ gets larger, the shape becomes more symmetrical and can be approximated by the normal distribution. The shape of the chi-square distribution depends on the number of degrees of freedom ‘ν’. The degrees of freedom (df) is equal to 24,because df n - 1 25 - 1 24.05 and df 2, the 2 critical value is 5.99. Since there are three intervention groups (flyer, phone call, and control) and two outcome groups (recycle and does not recycle) there are (3 1) (2 1) 2 degrees of freedom. The chi-square distribution is a continuous probability distribution with the values ranging from 0 to ∞ (infinity) in the positive direction. Example: Finding the critical chi-square value.Through this, it is clear that the chi-square has only one parameter, i.e. When a comparison is made between one sample and another, as in table 8.1, a simple rule is that the degrees of freedom equal (number of columns minus one) x (. The standard deviation is the square root of the variance: 15 2 2 15 2 30 5.477. The degrees of freedom (often abbreviated as df or d) tell you how many numbers in your grid are actually independent. The variance of a chi-square distribution is two times the degrees of freedom: 2 15 2 2 ( 15) 30. The probability function of Chi-square can be given as: Solution: The mean of a chi-square distribution is equal to the degrees of freedom: 15 2 k 15. One can show fairly easily that a simple rational function of a random variable with an F-distribution actually has a Beta distribution.The Sampling distribution of chi-square can be closely approximated by a continuous normal curve as long as the sample size remains large. The F-distribution with $\nu$ and $\xi$ degrees of freedom is $F=(\chi^2_\nu/\nu)/(\chi^2_\xi/\xi)$, where the two chi-square random variables are independent.
The F-distribution is one of the great work-horses of applied statistics. This comes up when one thinks about the F-distribution (The "F" stands for "Fisher", as in Ronald Aylmer Fisher, one of the most famous 20th-century scientists). This comes up when one thinks about the F-distribution (The 'F' stands for 'Fisher', as in Ronald Aylmer Fisher, one of the most famous 20th-century scientists). If we go back to this chart, we just learned that this probability from 6.25 and up, when we have three degrees of freedom, that this right over here is 10. If you find the probability that that random variable is $<1/2$, you'll get a far bigger number with a $\chi^2_1$ than with $\chi^2_/(2n)$.ĭividing the degrees of freedom by the chi-square random variable results in a distribution of quite a different shape, not merely a rescaled chi-square distribution. Dividing the degrees of freedom by the chi-square random variable results in a distribution of quite a different shape, not merely a rescaled chi-square distribution. So this right over here tells us the probability of getting a 6.25 or greater for our chi-squared value is 10.

The expected value does become the same as that of a $\chi^2_1$ distribution, but the shape of the density function is quite different. Dividing a chi-square-distributed random variable by its degrees of freedom is merely rescaling it doesn't change the shape parameter in the gamma distribution. The chi-squared distribution is implemented in the Wolfram Language as ChiSquareDistribution n.


 0 kommentar(er)
0 kommentar(er)
